Mathematical Design for Knotted Textiles
Abstract
This chapter examines the relationship between mathematics and textile knot practice, i.e., how mathematics may be adopted to characterize knotted textiles and to generate new knot designs. Two key mathematical concepts discussed are knot theory and tiling theory. First, knot theory and its connected mathematical concept, braid theory, are used to examine the mathematical properties of knotted textile structures and explore possibilities of facilitating the conceptualization, design, and production of knotted textiles. Through the application of knot diagrams, several novel two-tone knotted patterns and a new material structure can be created. Second, mathematical tiling methods, in particular the Wang tiling and the Rhombille tiling, are applied to further explore the design possibilities of new textile knot structures. Based on tiling notations generated, several two- and three-dimensional structures are created. The relationship between textile knot practice and mathematics illuminates an objective and detailed way of designing knotted textiles and communicating their creative processes. Mathematical diagrams and notations not only reveal the nature of craft knots but also stimulate new ideas, which may not have occurred otherwise.
Keywords
Design Knot diagram Knot theory Knotted textiles Rhombille tiling Wang tilesIntroduction: Mathematics and Textiles
Mathematics reveals facts inherent in nature, e.g., rotational symmetry of flowers, and fractals the system of arteries in the human body. Applications of mathematics can be found not only in biology, chemistry, and physics, but also in art, music, design, and architecture. Mathematical concepts have been adopted in the creation of various forms of art, ranging from geometrical sculptures to computer graphics. In return art can visually convey the phenomena of complex mathematical concepts to a wide audience, enabling people to understand things surrounding or even inside them.
In the field of textile art and design mathematics seems to have advanced the design of textiles, particularly in the field of technical textiles, e.g., models for entangled fibers (Lee and Ockendon 2005). Mathematics can also benefit the textile industry through the use of exact calculation (Woodhouse and Brand 1920, 1921). A more contemporary example is the “132 5. ISSEY MIYAKE” fashion collection that employed the mathematics of folding (Issey Miyake Inc 2018).
On the other hand, mathematicians have noticed the potential for the expression of mathematical concepts through textiles. A complex mathematical idea can be transformed into a material object to demonstrate proof of concept. Crocheting, knitting, and weaving are textile techniques that mathematicians often use to explore and communicate a variety of mathematical concepts. For example, the properties of the Lorenz Manifold are explicitly conveyed by through a crochet piece made from its computer-generated images (Osinga and Krauskopf 2004, 2014). Taimina (2009) uses crocheted models to illustrate the concept of hyperbolic geometry. Harris (1988, 1997) examines the mathematical content of various textile activities and illustrates how skills in mathematics can be acquired through the learning of textile crafts. She developed methods of teaching mathematics through looking at domestic textile craft objects. She used textiles to visualize mathematical concepts, such as symmetry, pairs, patterns, sets, lattices, tension, nets and solids, visual, tactile, and three-dimensional.
This chapter focuses on the relationship between knotted textiles and mathematics. It examines ways in which textile knot practice can be analyzed and discussed through the use of mathematics. Mathematical concepts involved in the analysis and discussion consist of knot theory (braid theory included), Wang tiling, and Rhombille tiling. The chapter aims to shed light on the relationship between these concepts with textile knot practice, especially how knot practice utilizes mathematical knot diagrams and tiling notations as design tools to generate novel knot structures and patterns that would not be created otherwise.
Textile Knot Practice to Be Analyzed
(Left) The White Forest (2016), dimensions: 150 cm(w) × 250 cm(d) × 200 cm(h); (Right) detail of tubular structure. Material: paper string. (Photograph: Nithikul Nimkulrat)
A single reef knot with two additional central strands passing through the center. (Photograph: Nithikul Nimkulrat)
A group of knots forming a circle. (Photograph: Nithikul Nimkulrat)
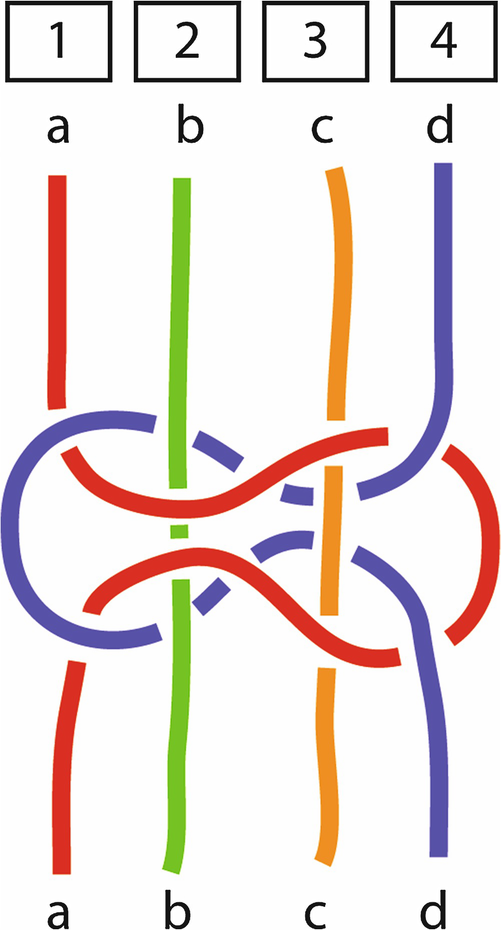
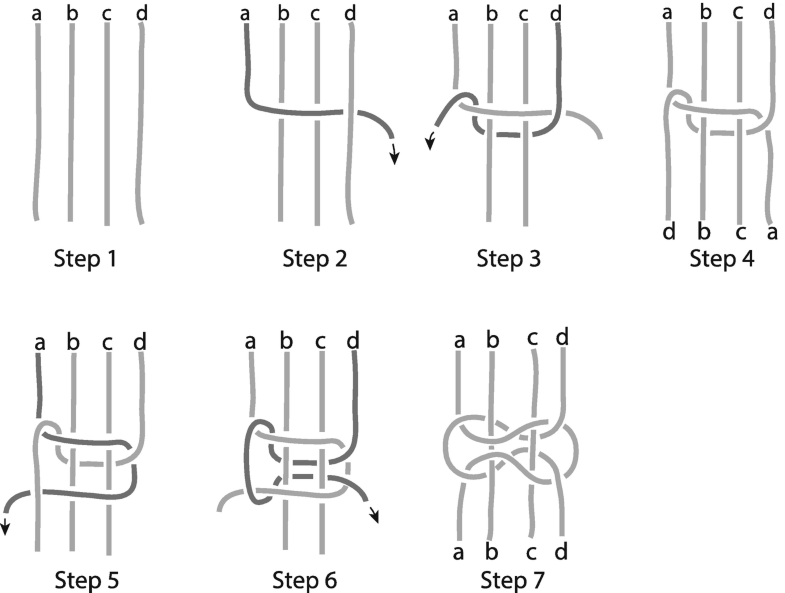
The design and process of knotting paper string into any three-dimensional forms in Nimkulrat’s knot practice prior to the work presented in this chapter was purely intuitive, as no sketch/drawing was made before the actual knotting. The knotting basically followed the rhythmic and coordinated movement of the left and right hands, employing tacit knowledge. As Sennett (2008: 94) points out: “… much of the knowledge craftsmen possess is tacit knowledge – people know how to do something but they cannot put what they know into words.” It is also the case of Nimkulrat’s knot practice. When communicating how knotting process was made, the articulation tended to be limited to “left hand over” or “right hand starting.” This has been transformed since Nimkulrat’s encountering with a mathematic knot diagram and wondered if there was any relationship between textile knots and mathematical knots and, if so, whether this would reveal ideas for new design and make the process of knotting more explicit. In order to characterize this knot in terms of mathematical knot theory, it is necessary to consider some of the properties of mathematical knots.
What is a Knot? Knot Theory and Its Diagrammatic Method
“Knotting has been an important adjunct to the everyday life of all people from the earliest days of which we have knowledge” (Ashley 1944: 1). Knots have been commonly used for nearly two thousand years for practical and decorative purposes in many cultures, such as Babylonian, Egyptian, Greek, Byzantine, Celtic, and Chinese art (Jablanand and Sazdanovic 2007). To a mathematician “a knot is a single closed curve that meanders smoothly through Euclidean three-space without intersecting itself” (van de Griend 1996: 205). It is a “closed loop in three-dimensional space,” which has “no free ends” (Devlin 1998: 248–249). To a textile practitioner, knotting or macramé is a craft technique commonly used in textile art and design. While free ends are essential for knotting textile work, “no string with free ends can be knotted” in mathematical knot theory, or topology (Devlin 1999: 234). This difference between craft and mathematical knots generates a question as to whether both types of knots share any similarities.
Knot theory is a subdivision of mathematical topology that examines properties of one-dimensional idealized objects, including knots, links, braids, and tangles (Adams 1994). These idealized objects consist of infinite thread and can be continuously deformed and reformed without breaking (Sossinsky 2002). The study of knots in mathematics focuses on properties relating to the positions of threads in space, the patterns of knots, and the number of crossings (Adams 1994: 2–4). It is not concerned with physical properties, such as tension, size, and the shape of individual loops (Devlin 1998: 247–249. A central problem in knot theory is to determine whether different representations are representations of equivalent (the same) knots. Solving this problem is concerned with seeking a property of each knot that does not change when the knot is subjected to manipulations. For each property, such as the number of crossings, a knot invariant might be defined (Devlin 1998: 249–254).
Equivalent representations of the same knot. (Diagrams: Janette Matthews)
In Fig. 4, each diagram is an equivalent representation of the same knot. The loop in the first diagram can gradually be removed to show a representation of the figure-eight knot in the fourth diagram.
Comparison Between Textile Knot Practice and Mathematical Knot Theory
A comparison between textile knot practice and mathematical knot theory
Property | Textile practice | Knot theory |
|---|---|---|
Ends | May have loose ends. | Continuous curve with no loose ends. |
Material | Textile material dependent, e.g., thickness, stiffness. | Not concerned with materiality. Cross section of a strand deemed to be a point. |
Tension | Textile practice dependent. A tight knot is very different from a loose knot. The space between is as important as the knot itself. | A tight knot has the same representation as a loose knot so they are deemed equivalent. |
Form | The addition of extra loops or turning a knot over changes its appearance. | If a knot may be simplified to the same representation of another knot, they are considered equivalent. |
Representation | A photograph or sketch. | Knot diagram. |
It can be seen in Table 1 that the differences between textile knot practice and mathematical knots are significant. However, in Nimkulrat’s practice, many of the differences may largely be ignored as the same knot, the same material, spacing, tension and form are employed consistently. The role of loose ends becomes the key difference for further consideration through two approaches, namely, through considering loose ends to be joined as they defined in mathematical knot diagrams and through braid theory, a further branch of topology, where loose ends are permitted.
The next sections will focus on the use of the diagrammatic method in knot theory to analyze textile knot practice in which physical strings are hand-knotted to create three-dimensional artifacts. They will show how diagrams can provide a visual language to interrogate and record practice, visualize or simulate new knot designs prior to making, and inspire the use of new materials.
Analysis of Textile Knot Practice Using Knot Theory
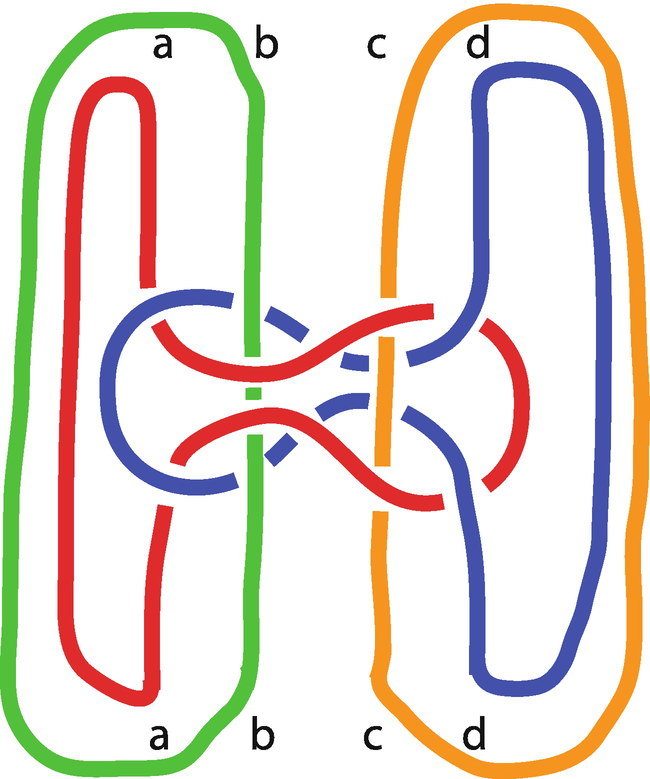
Knot diagram showing positions of strands of a single knot. (Diagram: Janette Matthews)
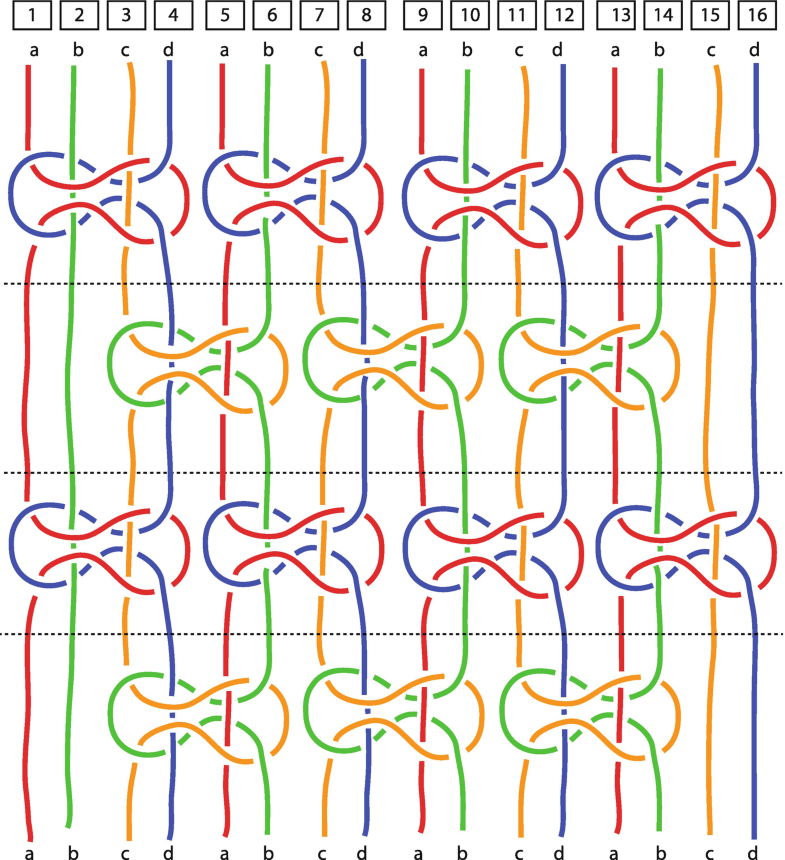
Diagram of four knots across and four knots down. (Diagram: Janette Matthews)
New Knot Pattern Designs Based on Knot Diagrams
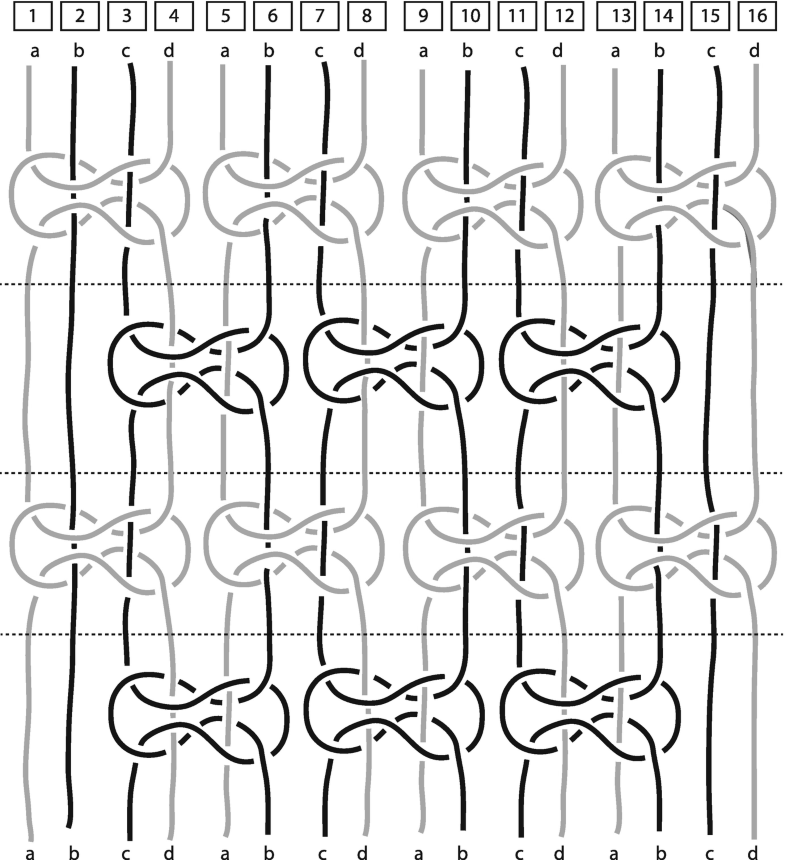
Figure 6 recolored using only two colors. (Diagram: Janette Matthews)
New knot design emerges when following Fig. 7 to knot black and white paper string. (Photograph: Nithikul Nimkulrat)
Black and white paper strings in a different position of strands generate a striped pattern. (Photograph: Nithikul Nimkulrat)
This step is an example of how diagramming can influence the design of knotted textiles that have always used one color to adopt two colors in textile knot practice.
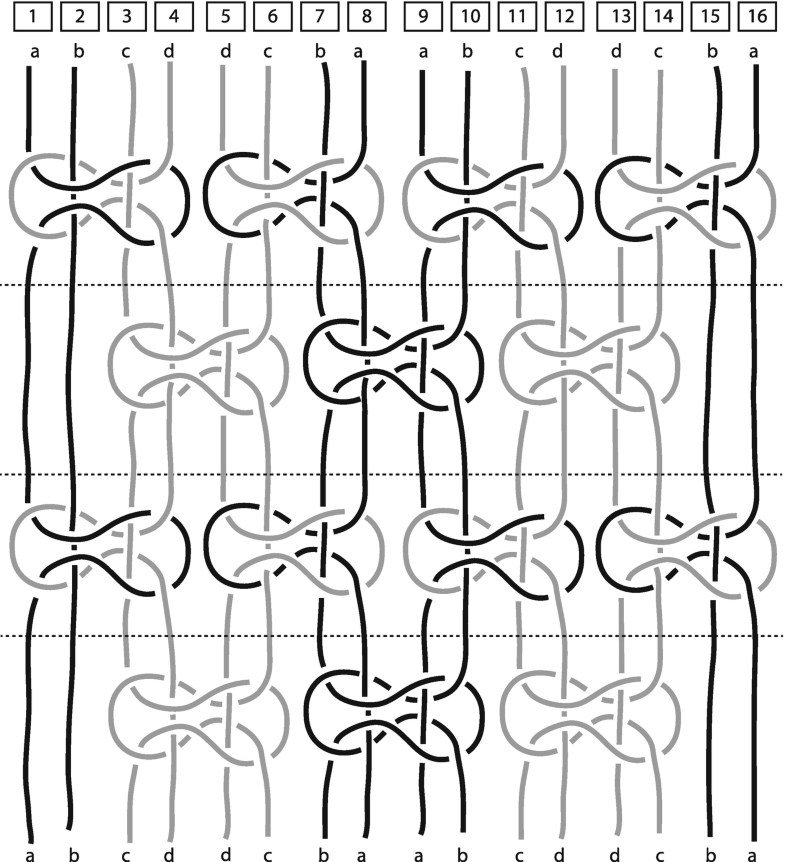
The subsequent knotting experiment puts the strands in the following positions from left to right: black–black–white–white (Fig. 9a). To link individual knots, one knot is flipped before the tying took place (Fig. 9b), allowing all four strings of the same color to form a pure color knot, black or white (Fig. 9c). The process continues alternately between a row of mixed color knots and that of pure black and white ones, leading to a striped knot pattern (Fig. 9d).
Diagram confirming the striped design in Fig. 9. (Diagram: Janette Matthews)
(Top) Black & White Striped Armchair (2014). Dimensions: 62 cm × 50 cm × 63 cm. (Bottom) Black & White Striped Knots (2015). Dimensions: 50 cm × 80 cm × 20 cm. (Photograph: Nithikul Nimkulrat)
Use of New Materials Inspired by Knot Theory
Knot theory also illuminates the use of a new material in Nimkulrat’s knot practice, encouraging her to work with materials and structures that she did not previously considered. The mathematical definition of a knot according to knot theory provides an opportunity to interrogate textile practice. The definition of a knot as closed curves with no loose ends (Devlin 1999) provokes an idea of using new materials.
Nimkulrat’s reef knot with all ends joined. It becomes a link of four trivial knots. (Diagram: Janette Matthews)
Four strands of neoprene cord tied into a knot whose ends are joined to create a link of four trivial knots. (Photograph: Nithikul Nimkulrat)
The unraveling of the individual knot with no loose ends creates four rings or trivial knots in the mathematics term. (Photograph: Nithikul Nimkulrat)
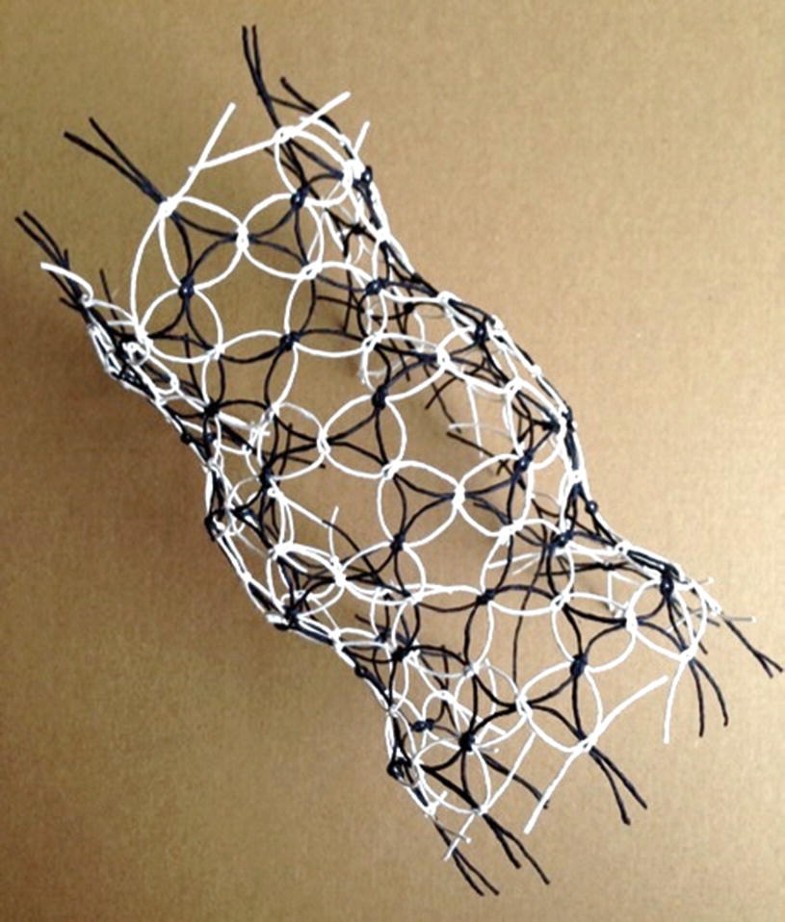
A new knotted structure made of neoprene cord. (Photograph: Nithikul Nimkulrat)
Analysis of Textile Knot Practice Using Braid Theory
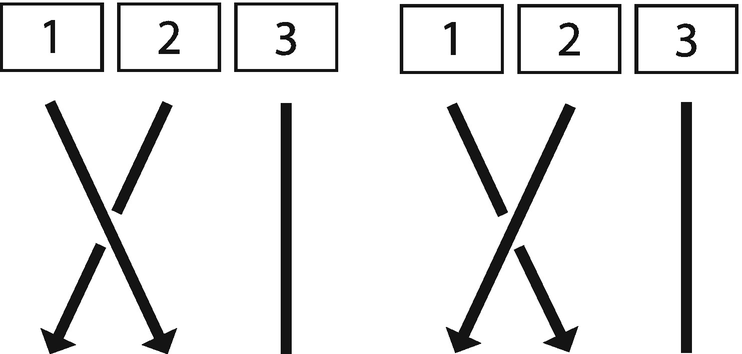
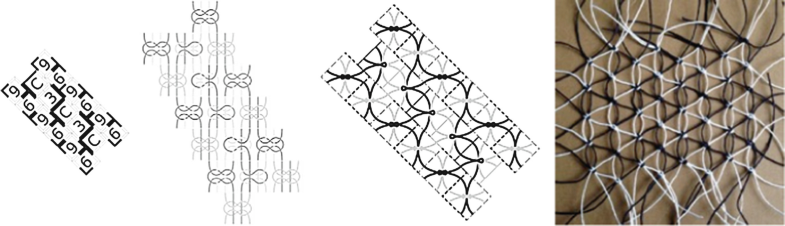
Representations of moves using Strands 1 and 2: Move “a” (left) and Move “A” (right). (Diagram: Janette Matthews)
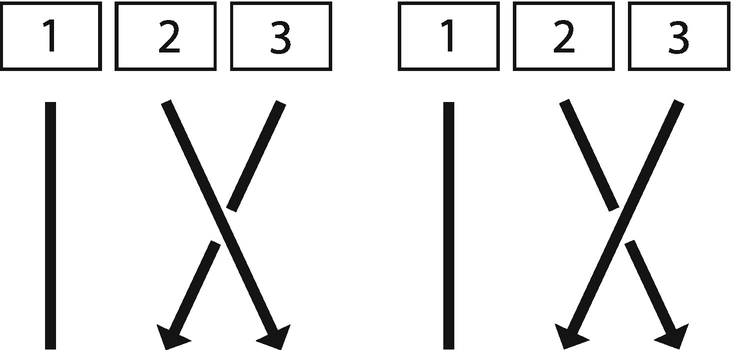
Representations of moves using Strands 2 and 3: Move “b” (left) and Move “B” (right). (Diagram: Janette Matthews)
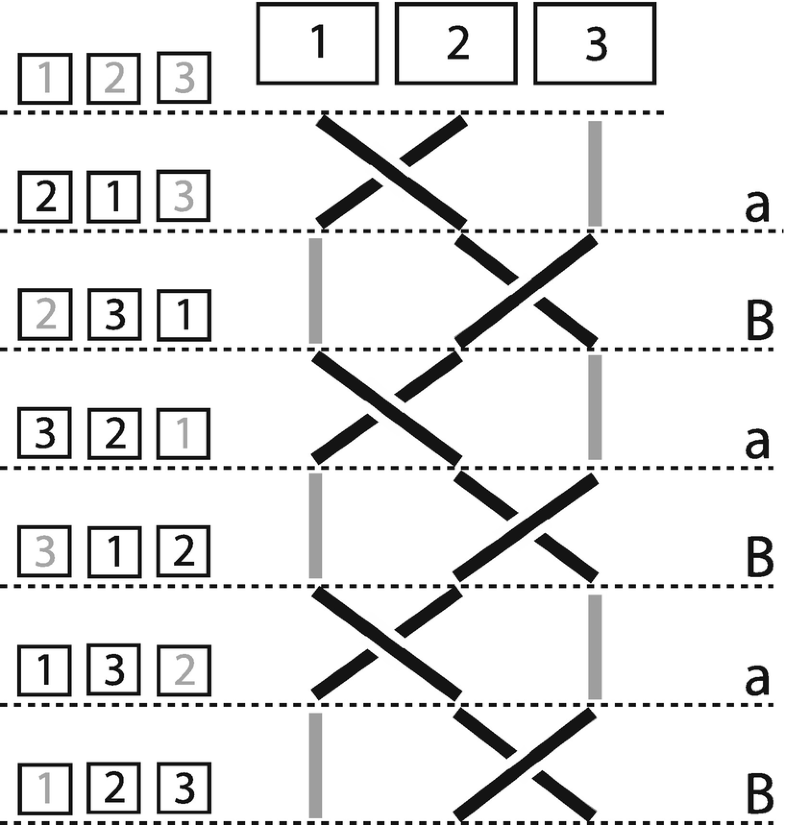
A braid diagram for the simple plait and algebraic notation for each move. (Diagram: Janette Matthews)
Steps involved in tying a knot in Fig. 2. (Diagram: Janette Matthews)
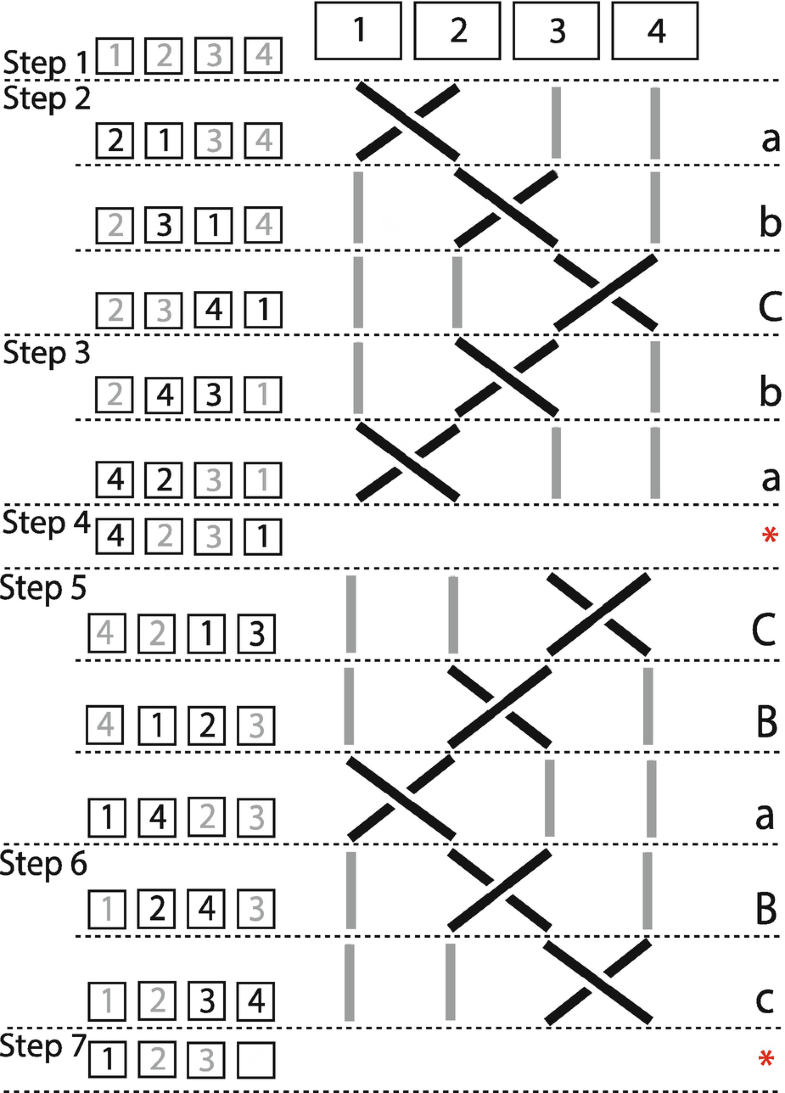
The modified braid diagram for Nimkulrat’s knot. (Diagram: Janette Matthews)
In the formulation of the braid notation in Fig. 20, to complete Steps 3 and 6, the strand must first move upwards the braid to pass through a loop to tie the knot. Such a move is not permitted in braid theory that, by definition, all moves must be in a downward direction. This indicates that pure braid theory cannot be used to characterize the craft knot in question. In order to continue the analysis of this knot using braid theory, the theory is therefore modified to allow the upward move. The notation given for this move is *, which refers to not only the upward move of the strand that is last twisted over in the previous move, but also the passing of it through a loop created by the strand twisting over it. The notation that describes the knotting process of the Fig. 2 knot is abCba*CBaBc*.
Definition of Tilings
The mathematical theory of tilings has to do with covering two-dimensional Euclidean spaces with tiles of various forms without gaps or overlays (Kaplan 2009: 3). Topologically individual tiles are closed continuous disks. A tiling is periodic if it is made up of regions of any size that repeat one after another. The shape of the tiles is arbitrary. Simple elements are regular triangular, square, and hexagonal tiles. The tiles may have matching conditions dictating which may be placed next to each other. These may be implemented as dents and notches but are usually indicated by various colors and coded with numbers.
The set of different kinds of available tiles is called a protoset. The individual tiles in a protoset are called prototiles (Mann 2004). An infinite number of copies of any tile may be used in the tiling. If a protoset can be used to tile the entire Euclidian plane, it is called valid. Each of the aforementioned tiles forms by themselves a valid set. There are also protosets that cannot be used to tile the plane, like the single pentagonal tile. A valid set that allows no regular tilings is an aperiodic set. Although the tiling theory is concerned with the Euclidian plane, the question may be asked about any surfaces. For example, we might be looking for a tiling that covers the surface of a finite cube or infinitely long cylinder. Also the tilings have topologies. For example, the regular square tiling is different from hexagonal tiling. On the other hand, tilings that look different may have similar properties. For example, a brick wall tiling has the same topology as the regular hexagonal tiling, even when the prototiles have different shapes.
An important special case includes the Wang tiles. Mathematically they are defined as unit squares with colored edges and the following matching conditions: (1) tiles may not be mirrored or rotated; (2) they are to be placed in the regular square grid; and (3) touching edges must have the same color (Lagae and Dutre 2006; Nurmi 2016). Regular, aperiodic, and invalid Wang tilesets are known. Since the definition is mathematical and the colors are defined by colors, which in turn may be implemented by shaping the edges, shapes of their actual representations may vary greatly.
Analysis of Textile Knot Practice Using Tilings
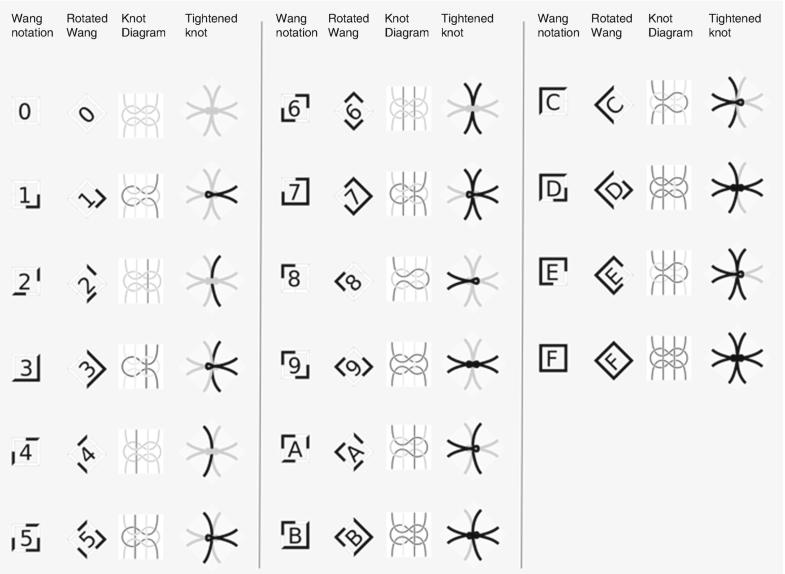
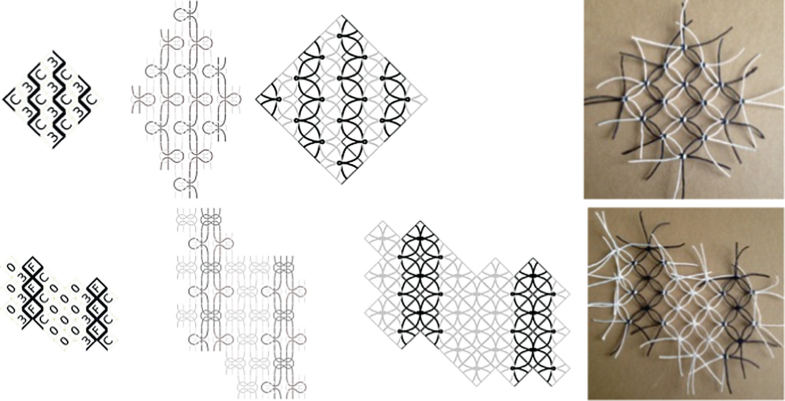
The 16 knot units identified. (Diagram: Tuomas Nurmi)
The first column of Fig. 21 shows the canonical forms of the Wang tiles. As the actual knot patterns are in 45° angle, the second column shows the rotated tile, and the third the corresponding knot diagram. The fourth shows what an individual tightened physical knot would look like.
New Pattern and Structure Designs Based on Tiling Concepts
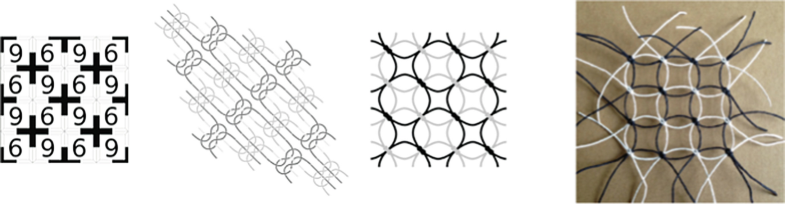
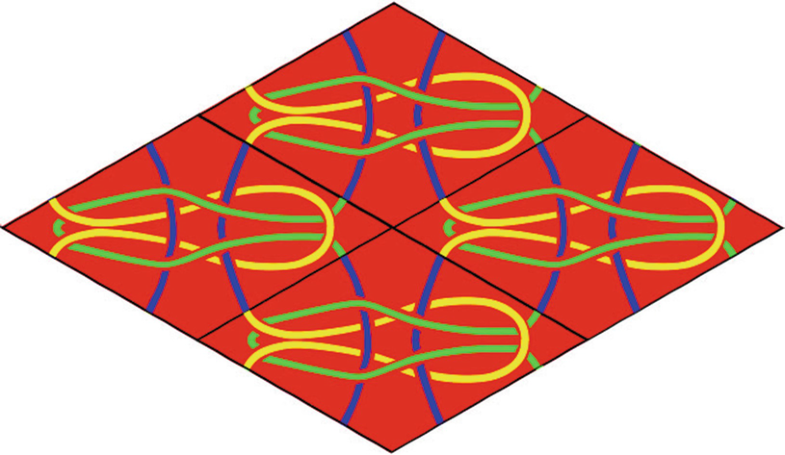
From left: pattern as Wang tiles (6 and 9 in combination), generated knot diagram, predicted, and actual outcome. (Diagram: Tuomas Nurmi. Photograph: Nithikul Nimkulrat)
Tiling-based designs and sample knots of two stripe patterns. (Diagram: Tuomas Nurmi. Photograph: Nithikul Nimkulrat)
Tiling-based design that discards the Wang square grid topology. (Diagram: Tuomas Nurmi. Photographs: Nithikul Nimkurat)
The design in Fig. 24 using three colors instead of two. (Photograph: Nithikul Nimkulrat)
Three-dimensional knot structure based on color coded tiling design. (Diagram: Tuomas Nurmi. Photographs: Nithikul Nimkurat)
In the next phase, the notion of square grid is abandoned and patterns are explored based on the Rhombille tiling. The opposite corners of a Rhombille tile are 60° or 120°. This property seems to have potential to generate novel knot designs that have different structures and characteristics.
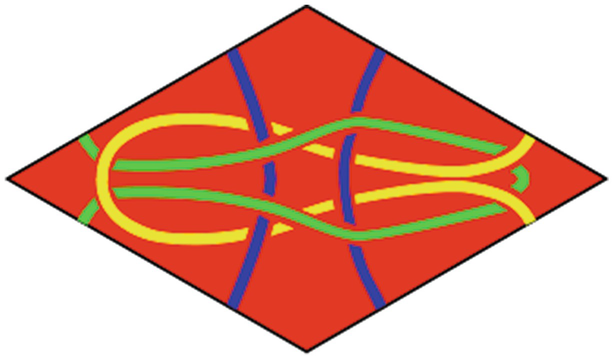
A single prototile coding a single knot diagram. The passive strands are in one color and the active strands are in two different colors. (Diagram: Tuomas Nurmi)
Rhombille tiling of a reef knot. (Diagram: Tuomas Nurmi)
Knotted work following Fig. 28. (Photograph: Nithikul Nimkulrat)
Rhombille tiling of a reef knot – second variation. It combines the Rhombille tiling with a different type of isohedral tilings – P4-55. (Diagram: Tuomas Nurmi)
Knotted work following Fig. 30. (Photograph: Nithikul Nimkulrat)
Four prototiles placed according to the P4-55 tiling rule to form a larger tile. (Diagram: Tuomas Nurmi)
Rhombille tiling of a reef knot – third variation. It integrates a different type of isohedral tilings P4-55 into the Rhombille tiling. (Diagram: Tuomas Nurmi)
Knotted work following Fig. 33. (Photograph: Nithikul Nimkulrat)
Conclusion
This chapter demonstrates that it is possible to explore textile knot practice through the application of mathematics, especially knot theory and tiling concepts.
First, knot theory may be used to examine the properties of knotted textile structures, revealing significant differences between textile craft knots and knots in mathematical knot theory. Second, textile knot practice can adopt the diagrammatic method commonly used in mathematical knot theory as a design tool. Through the coloring of knot diagrams, the positions and roles of strands in a knotted structure become explicit, triggering an exploration of two-tone knot pattern designs. Third, the mathematical characterization of a single craft knot can inspire a new choice of material for knot practice, leading to a new design of knotted textiles with no loose ends. Fourth, modified braid theory can be used to characterize the same craft knot. Although mathematical braid theory in its pure form is invalid as no upward moves are permitted by definition, the characterization of the craft knot in question using a modified theory is useful because it explicitly shows the upward knotting move which is not otherwise obvious. Last, tiling notations that follow the Wang tiling concept and the Rhombille tiling rule can be used as design tools in textile knot practice to generate new knot patterns and structures.
The understanding of mathematical properties of craft knots can facilitate the communication of creative processes in a more objective and detailed way. Mathematical diagrams and notations reveal the nature of a particular knot types and stimulate new ideas, which may not have occurred otherwise. They may be used to design a variety of knotted textile structures that are visually different from one another, yet adopting only a single type of knot in a topological sense.
For future work, there are simple ways to extend tiling based design beyond this work. The braid theory suggests an infinite number of strands flowing in parallel and crossing each other. These may be modeled by knot diagrams running in parallel. These in turn may be reverse engineered into rectangular tiles with colored edges, which allows creative use of the color matching method. On the other hand, the method might be used in different types of tiling. For example, it is easy to create knot diagrams for the two tiles in the aperiodic P3 tiling.
Further, in these examples only one type of knot – the reef knot – is used. The tiles used may have different shapes, numbers of edge colors, and different numbers of colors on the edges. By definition the tiles are ignorant about their decoration and only care about the edge colors. Thus, several tiles with the same edge colors, but different diagrams, may even be achieved.
References
- Adams C (1994) The knot book: an elementary introduction to the mathematical theory of knots. W H Freeman, New YorkzbMATHGoogle Scholar
- Ashley CW (1944) The Ashley book of knots. Faber and Faber, LondonGoogle Scholar
- Devlin K (1998) The language of mathematics: making the invisible visible. W H Freeman, New YorkzbMATHGoogle Scholar
- Devlin K (1999) Mathematics: the new golden age. Columbia University Press, New YorkzbMATHGoogle Scholar
- van de Griend P (1996) A history of topological knot theory. In: Turner JC, van de Griend P (eds) History and science of knots. World Scientific, Singapore, pp 205–260CrossRefGoogle Scholar
- Grünbaum B, Shephard GC (1987) Tilings and patterns. W H Freeman, New YorkzbMATHGoogle Scholar
- Harris M (1988) Common threads: mathematics and textiles. Math Sch 17(4):24–28Google Scholar
- Harris M (1997) Common threads: women, mathematics and work. Trentham Books, Stoke-on-TrentGoogle Scholar
- Issey Miyake Inc (2018) 132 5. Issey Miyake. http://www.isseymiyake.com/en/brands/132_5.html. Accessed 20 July 2008
- Jablanand S, Sazdanovic R (2007) LinKnot: knot theory by computer, vol 21. World Scientific, SingaporeCrossRefGoogle Scholar
- Kaplan CS (2009) Introductory tiling theory for computer graphics. Morgan & Claypool, San RafaelCrossRefGoogle Scholar
- Lagae A, Dutre P (2006) An alternative for Wang tiles: colored edges versus colored corners. ACM Trans Graph 25(4):1442–1459CrossRefGoogle Scholar
- Lee MEM, Ockendon H (2005) A continuum model for entangled fibres. Eur J Appl Math 16:145–160MathSciNetCrossRefGoogle Scholar
- Mann C (2004) Heesch’s tiling problem. Am Math Mon 111(6):509–517MathSciNetCrossRefGoogle Scholar
- Meluzzi D, Smith DE, Arya G (2010) Biophysics of knotting. Annu Rev Biophys 39:349–366CrossRefGoogle Scholar
- Nimkulrat N (2009) Paperness: expressive material in textile art from an artist’s viewpoint. University of Art and Design Helsinki, HelsinkiGoogle Scholar
- Nimkulrat N, Matthews J (2016) Novel textile knot designs through mathematical knot diagrams. In: Torrence E, Torrence B, Séquin C, McKenna D, Fenyvesi K, Sarhangi R (eds) Proceedings of Bridges 2016: mathematics, music, art, architecture, education, culture. Tessellations, Phoenix, pp 477–480Google Scholar
- Nurmi T (2016) From checkerboard to cloverfield: using Wang tiles in seamless non-periodic patterns. In: Torrence E, Torrence B, Séquin C, McKenna D, Fenyvesi K, Sarhangi R (eds) Proceedings of Bridges 2016: mathematics, music, art, architecture, education, culture. Tessellations, Phoenix, pp 159–166Google Scholar
- Osinga HM, Krauskopf B (2004) Crocheting the Lorenz manifold. Math Intell 26(4):25–37MathSciNetCrossRefGoogle Scholar
- Osinga HM, Krauskopf B (2014) How to crochet a space-filling pancake: the math, the art and what next. In: Greenfield G, Hart GW, Sarhangi R (eds) Bridges 2014: mathematics, music, art, architecture, culture. Tessellations, Phoenix, pp 19–26Google Scholar
- Sennett R (2008) The craftsman. Yale University Press, New HavenGoogle Scholar
- Sossinsky A (2002) Knots: mathematics with a twist. Harvard University Press, Cambridge, MAzbMATHGoogle Scholar
- Taimina D (2009) Crocheting adventures with hyperbolic planes. AK Peters, WellesleyCrossRefGoogle Scholar
- Woodhouse T, Brand A (1920) Textile mathematics: part I. Blackie & Son, LondonGoogle Scholar
- Woodhouse T, Brand A (1921) Textile mathematics: part 2. Blackie & Son, LondonGoogle Scholar